Quantification of Uncertainties in Neural Networks

Neural network (NN) have recently been an extremely popular choice as surrogates to complex physical models. However, in most instances trained NNs are treated deterministically. Probabilistic approaches to ML, particularly NNs, provide the necessary regularization of the typically overparameterized NNs while leading to predictions with uncertainty that are robust with respect to the amount and quality of input data.

In the context of probabilistic estimation, Bayesian methods provide an ideal path to infer NN weights while incorporating various sources of uncertainty in a consistent fashion. However, exact Bayesian posterior distributions are extremely difficult to compute or sample from. Variational approaches, as well as ensembling methods, provide viable alternatives accepting various degrees of approximation and empiricism.

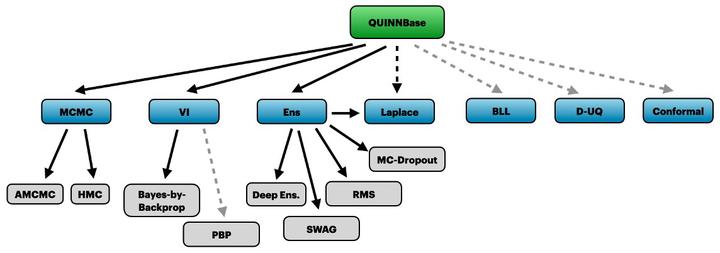
We have developed a software library Quantification of Uncertainties in NNs (QUiNN) that consists of probabilistic wrappers around PyTorch NN modules, to enable exploration of NN loss surfaces and the accuracy of several UQ-for-NN approaches, including Hamiltonian Monte-Carlo, Laplace approximation, variational approximations, ensemble methods.

Figure
Implemented and planned methods in QUiNN.

Acknowledgements
This work has been supported by SNL LDRD program, as well as DOE Office of Science ASCR program.