Embedded Model Error Propagation and Attribution

The calibration of computational models of physical systems typically assumes that the computational model replicates the exact mechanism behind data generation. As a result, calibrated model parameters are often biased, leading to deficient predictive skills. We developed a Bayesian inference framework for representing, quantifying, and propagating uncertainties due to model structural errors by embedding stochastic correction terms in the model [1, 2]. The embedded correction approach ensures physical constraints are satisfied and renders calibrated model predictions meaningful and robust with respect to structural errors over multiple, even unobservable, quantities of interest. The physical inputs and correction parameters are simultaneously inferred via surrogate-enabled Markov chain Monte Carlo. With a polynomial chaos characterization of the correction term, the approach allows efficient decomposition of uncertainty that includes contributions from data noise, parameter posterior uncertainty, and model error.

The developed structural error quantification workflow is implemented in UQ Toolkit. We applied this method in a range of practical applications of DOE interest including fusion science [3, 4], fluid dynamics [5, 6], structural engineering [7, 8], materials science [9].

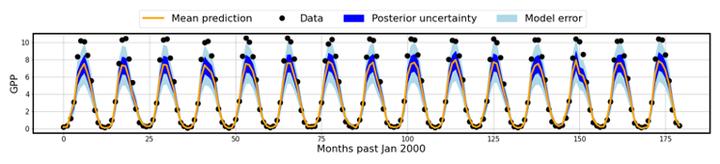
Figure
Demonstration of embedded model error correction to a climate land model output, gross primary productivity (GPP).

Acknowledgements
This work is largely supported by DOE SciDAC FASTMath institute.

References
[1] K. Sargsyan, H. N. Najm, R. Ghanem, “On the Statistical Calibration of Physical Models”, International Journal for Chemical Kinetics, 47:4, pp. 246–276, 2015.

[2] K. Sargsyan, X. Huan, H. N. Najm. “Embedded Model Error Representation for Bayesian Model Calibration”, International Journal of Uncertainty Quantification, 9:4, pp. 365–394, 2019.

[3] T.R. Younkin, K. Sargsyan, T. Casey, H.N. Najm, J.M. Canik, D.L. Green, R.P. Doerner, D. Nishijima, M. Baldwin, J. Drobny, D. Curreli, B.D. Wirth, “Quantification of the effect of uncertainty on impurity migration in PISCES-A simulated with GITR”, Nuclear Fusion, 62:5, p.056007, 2022.

[4] O. Cekmer, K. Sargsyan, S. Blondel, H. Najm, D. Bernholdt,, B.D. Wirth, “Uncertainty quantification for incident helium flux in plasma-exposed tungsten”, International Journal for Uncertainty Quantification, 8:5, pp.429–446, 2018.

[5] X. Huan, C. Safta, K. Sargsyan, G. Geraci, M. S. Eldred, Z. P. Vane, G. Lacaze, J. C. Oefelein, Habib N. Najm, “Global Sensitivity Analysis and Estimation of Model Error, toward Uncertainty Quantification in Scramjet Computations”, AIAA Journal, 56:3, pp.1170–1184, 2018.

[6] C. Safta, M. Blaylock, J. Templeton, S. Domino, K. Sargsyan, H. Najm, “Uncertainty Quantification in LES of Channel Flow”, International Journal for Numerical Methods in Fluids, 83, pp.376–401, 2016.

[7] F. Ghahari, K. Sargsyan, G. Parker, D. Swensen, M. Celebi, H. Haddadi, E. Taciroglu, “Performance Based Earthquake Early Warning for Tall Buildings”, Earthquake Spectra, 40:2, 2024.

[8] F. Ghahari, K. Sargsyan, M. Celebi, E. Taciroglu, “Quantifying modeling uncertainty in simplified beam models for building response prediction”, Structural Control and Health Monitoring, 29:11, p.e3078, 2022.

[9] A. Hegde, E. Weiss, W. Windl, H.N. Najm, C. Safta, “A Bayesian Calibration Framework with Embedded Model Error for Model Diagnostics”, International Journal for Uncertainty Quantification, 2024.